Knalltrauma.ch

Start Lautstärke Theorie Folgen Aufklärung Download

Marderschreck, Katzenschreck, Hörschaden, Burnout, Tinnitus, ADHS www.knalltrauma.ch

A-Filter: Beurteilung von Musik oder Lärm mit dB(A)

Mit dB(A) die Gefahr eines Hörschadens bestimmen ist etwa das Gleiche wie aus einem Totalbetrag eines Kassenzettels den Einkauf rezitieren. Totalbeträge können einfach verglichen werden, aber nur mit den Totalbeträgen bestimmen was und wie viel davon eingekauft wurde ist ein Ding der Unmöglichkeit. Mit Dezibel wird die Unmöglichkeit einfach noch etwas komplizierter. Für jede Frequenz gibt es einen eigenen Korrekturfaktor und fürs Zusammenzählen muss von logarithmisch auf linear gewechselt werden.

Will man wissen, wie viel Energie ein Ton hat, nimmt man Dezibel. Damit weiss man jedoch noch nicht, wie laut dieser Ton empfunden wird. Das menschliche Hörempfinden ist kompliziert. Gleich viel Dezibel tönen nicht für alle Töne gleich laut. Zudem ändert es auch noch mit der Lautstärke. Um die empfundenen Lautstärken vergleichen zu können, wurde deshalb vor sehr langer Zeit, zu einer Zeit als es noch keine Schreckgeräte gab, der 1 kHz Ton bei einer Lautstärke von 40 dB als Referenz genommen und für alle andern Töne durch Zugabe oder Wegnahme von einigen wenigen Dezibel auf gleich laut empfundene Lautstärke für durchschnittliche Erwachsenen eingestellt. Bei gleich viel dB(A) sollten durchschnittliche Erwachsenen die leisen Töne alle als etwa gleich laut wahrnehmen, bei gleich viel dB(C) die lauten Töne alle als etwa gleich laut empfinden.

In der ISO 226 ist die unterschiedliche Lautstärkeempfindung des gesunden Gehörs für verschiedene Frequenzen, bei verschiedenen Lautstärken, festgehalten. Damit die empfunden Lautstärken etwas bequemer verglichen werden können, wurden A,B,C und D Filter entwickelt. Gebräuchlich sind noch A und C Filter:

Mit dem A-Filter wird das menschliche Hörverhalten bei leisen Tönen verglichen. 40 dB(A) sollten für jede Frequenz in etwa gleich laut sein.
Fälschlicher Weise wird behauptet:
Die Hörschwelle sei 0 dB(A), die Schmerzgrenze sei 130 dB(A).

Die Hörschwelle und die 0 dB(A) Kurve (grün) haben wenigstens einen ähnlichen Verlauf.
Die Schmerzgrenze und die 130 dB(A) Kurve (rot) verlaufen hingegen in entgegengesetzten Richtungen.

Der A-Filter wurde vor vierzig Jahren mit relativ wenig elektrischen Bauteilen realisiert. Er ermöglicht einfache und brauchbare Vergleiche der empfundnen Lautstärken für Sprache und Musik. Er hat sich wegen seiner einfachen Handhabung vor Gericht durchgesetzt. Mit dB(A) werden Musik, Strassenlärm, oder auch einzelne Töne verglichen. Die Resultate sind brauchbar für Lärmbelästigung und Ruhestörung.

Wie und wo das Gehör belastet wird, kann mit einem dB(A) Wert nicht angegeben werden. Rechnet man bei tiefen und hohen Frequenzen mit dB(A), sind Hörschäden vorprogrammiert!

Bewertung mit dem A-Filter

In den Kurven gleicher Lautstärke (ISO 226) ist festgehalten, wie viel dB es jeweils bei verschiedenen Lautstärken braucht, damit die verschiedenen Töne gleich laut empfunden werden. Die Einheit für die empfundene Lautstärke ist das Phon. Referenz für die Phonkurve ist die Frequenz 1 kHz, wo der Phon Wert dem dB Wert entspricht (1Phon = 1dB). Sehr grob vereinfacht wird mit dem A-Filter die 40 Phon Kurve (rot) in eine 40 dB(A) Gerade (blau) umgewandelt.

Der Unterschied zwischen dB und dB(A) ist nur eine Tabelle.
Es gibt nicht nur den A-Filter. Definiert sind auch die Bewertungen B-, C- und D-Filter. Heutzutage sind jedoch nur noch A- und C-Filter in Gebrauch.
Mit der A-Bewertung ergeben sich bei ungefähr gleich laut empfundenen Lautstärken ähnliche dB(A)-Anzeigen.
Die exakte A- und C-Bewertung ist in der Tabelle vom "dBA-Rechner" von sengpielaudio hinterlegt.
Nachfolgende Graphik und die Tabellenausschnitte sind diesem dBA-Rechner entnommen:

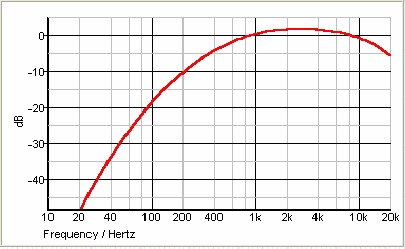
Die Filter addieren oder subtrahieren für jede Frequenz einen konstant vorgegebenen Wert zur gemessenen Lautstärke. Dieser Wert ist unabhängig von der Lautstärke, deshalb laufen alle dB(A) Kurven parallel. Beispiel die zuoberst im Diagramm Hörfläche eingezeichneten Kurven für 0 dB(A) "Hörschwelle", 130 dB(A) "Sch(m)erzgrenze", sowie die blau eingezeichneten Kurven für 40 dB(A), 70 dB(A) und 100 dB(A).

Addieren von dB oder dB(A)

Das Dezibel (dB) ist ein logarithmisches Mass. Addieren wir dB, machen wir in Wirklichkeit eine Multiplikation, subtrahieren wir dB, ist dies eine Division. Wenn wir z.B. mit dem A-Filter 6 dB weniger bewerten, rechnen wir in Wirklichkeit mit einem Viertel der effektiven Leistung.
Möchte man die "Lautstärken" von Frequenzen oder Geräuschen zusammenzählen, dann muss man zuerst ins lineare Zahlensystem zurück, dann die linearen Werte addieren und anschliessend erst wieder in das logarithmische Mass dB Rückumwandeln.

Beispiel: Addition der dB von den drei Frequenzen f1 = 50 dB, f2 = 52 dB und f3 = 53 dB
Raus aus logarithmischen in das lineare Zahlenverhältnis .
Linear1 = 10^(f1/10) = 10^(50dB/10) = 10^5 = 100000.
Linear2 = 10^(f2/10) = 10^(52dB/10) = 10^5.2 = 158489.
Linear3 = 10^(f3/10) = 10^(53dB/10) = 10^5.3 = 199526.
Die drei Werte addieren, ergibt L = L1 + L2 + L3 = 458015 zu erhalten.
Nun zurück zu dB: L = 10 · log (458015 ) = 56,6 dB.

A-Filter berücksichtigt Hörschwelle, aber nicht Schmerzgrenze

Die 40-phon Kurve ist die Basis für den A-Filter und verläuft ungefähr parallel zur Hörschwelle. Weil das A-Filter den ungefähren Verlauf der Hörschwelle berücksichtigt, ergeben sich brauchbare Resultate für die empfundenen Lautstärken.
Für die Gehörsgefährdung müssten wir jedoch die Schmerzschwelle berücksichtigen. Dort wo die Schmerzgrenze sinkt, steigt die Hörschwelle. Der A-Filter korrigiert bei der Gefahr von Hörschäden in die falsche Richtung!

Der A-Filter ist zum Bestimmen der Gehörsgefährdung vollkommen unbrauchbar. Die identische Anzeige von 100 dB(A) für die drei Frequenzen 20 Hz, 2 kHz und 20 kHz entspricht in Wirklichkeit.
20 Hz = 150.5 dB , 2 kHz = 98.8 dB,20 kHz = 107.5 dB
Bei der Frequenz 2 kHz haben wir am meisten Reserve bis zur Schmerzgrenze und das Messgerät zeigt etwas zuviel an. Bei 20 Hz und 20 kHz sind wir über der Schmerzgrenze und das Messgerät zeigt zuwenig an.

Schmerz warnt uns vor Gefahr. Bei hohen und tiefen Frequenzen ist die Schmerzgrenze tiefer. Das Messgerät müsste bereits bei weniger dB Alarm schlagen und zuviel anzeigen. Stattdessen wird bei hohen und tiefen Frequenzen Entwarnung gegeben und zuwenig angezeigt!

Aber wieso ist dann ein solch katastrophaler Filter in Gebrauch? Der A-Filter wurde vor ungefähr vierzig Jahren entwickelt. Damals gab es kaum Taschenrechner. Die Bewertungskurve war technisch relativ kostengünstig zu realisieren und deckte die damaligen Bedürfnisse gut ab. Es ging um Lärmbelästigung. Nicht um Gehörsgefährdung. Damals gab es noch keine Marderschäden. Es gab auch keine Marderschreckgeräte. Die ultra hohen Frequenzen in den riesigen Lautstärken kamen damals in der freien Natur nirgends vor.